Ing. Eliany de la Caridad Valera Sterling1,2, Dr.C. Eduardo García Noa2,*, Dr.C.  Lourdes Mariana Crespo Zafra3

1Centro de Gestión de la Información y Desarrollo de la Energía, (Cubaenergía), La Habana, Cuba. ORCID https://orcid.org/0000-0002-6655-5637

2Universidad Tecnológica de La Habana (Cujae), La Habana, Cuba;                   egarcianoa@quimica.cujae.edu.cu. ORCID: https://orcid.org/0000-0002-6634-9219

3Departamento de Ciencia y Tecnología de los Alimentos, Fac. Ciencias Aplicadas, Universidad de Camaguey Ignacio Agramonte Loynaz, ORCID:https://orcid.org/0000-0002-4799-3447

*Correspondencia: egarcianoa@quimica.cujae.edu.cu; Telf.: (53) 5622 5798

DOI: 10.70373/RB/2024.09.03.11

En la producción de yogur natural hay un alto consumo de energía, no obstante, en algunas etapas del proceso no se hace un uso racional de los portadores energéticos; por lo que para reducir los consumos y disminuir las pérdidas, se definió como objetivo establecer las condiciones de operación con mayor eficiencia energética, integrando la optimización multiobjetivo con la simulación mediante modelos multivariados. Se estudiaron 10 producciones y el procedimiento incluyó el cálculo de los índices de consumo de vapor, de agua y el índice de pérdidas de materiales, dichos valores fueron 0,1384, 6,621 y 0,0192, respectivamente. Se aplicaron los métodos multivariados para establecer la relación entre la masa de yogur y los índices calculados con 14 variables de operación. Los modelos de Mínimos Cuadrado Parciales presentaron un error cuadrático de predicción inferior a 4,746. Para estimar la condición de operación de mayor eficiencia, se empleó la optimización multiobjetivo; lográndose el óptimo global en aquella en que la masa de yogur fue 3 582 kg. Debiéndose tener un control riguroso sobre el inóculo, la temperatura de refrescamiento del cultivo, la leche fermentada, y la masa de yogur ya que estas variables presentaron el mayor peso sobre las cuatro variables dependientes.

Palabras claves: optimización multiobjetivo, modelos multivariados, yogur natural batido, índices de consumo, pérdidas de materiales

In the natural yogurt production there is a high consumption of energy; nevertheless, in some of the stages there are not a rational use of energy; To reduce the consumptions and reduce losses, the objective was defined to establish operating conditions with high efficiency, integrating the multi-objective optimization with the multivariate models simulation. Were studied 10 productions and the procedure included the calculation of the total consumption rates of steam and water, and the material loss rate, these values were 0.1384, 6.621 and 0.0192, respectively. Multivariate methods were applied to establish the relationship between the yogurt mass and of the calculated rates with 14 operating variables; The models adjusted by Partial Least Squares were obtained with a lower quadratic prediction error equal to 4.746. Finally, to estimate the operating condition that increases efficiency, multi-objective optimization was used; where the operating condition in which the global optimum is achieved is that in which the mass of yogurt was 3 582 kg. Therefore, rigorous control must be taken during production on the inoculum, the cooling temperature of the technical culture, the fermented milk, and the whipped yogurt mass because these variables presented the greatest weight on the four dependent variables.

Keywords: multi-objective optimization, multivariate models, whipped natural yogurt, consumption rates, material loss rate.

La producción de yogur natural batido conlleva un alto consumo energético, por lo que es importante que se utilice la energía racionalmente, no obstante, hay etapas del proceso que no hacen un uso óptimo de los portadores energéticos1. Dada la potencialidad existente de reducir los consumos y las pérdidas, se partió de la hipótesis de que es posible con la integración de la optimización multiobjetivo2,3 y la simulación mediante modelos multivariados, establecer condiciones de operación que incrementen la eficiencia energética.

Para valorar el desempeño de un proceso se debe contar con índices que muestren las desviaciones en los consumos4 y, por otra parte, el análisis de datos puede incluir métodos multivariantes5 para estudiar variables correlacionadas. Entre ellos el análisis de conglomerados, el análisis de componentes principales y los mínimos cuadrados parciales 6,7,8.

Se debe tener en cuenta que la mejora de procesos tecnológicos requiere la optimización simultánea9 de varios objetivos que compiten entre sí; estos problemas se caracterizan por una gran complejidad del espacio de decisión, en estos casos puede ser útil la optimización multiobjetivo, que es una técnica10 que permite mejorar varios criterios en un proceso simultáneamente. Un modelo multiobjetivo puede transformarse en uno equivalente, mediante la maximización de la variable auxiliar en una función de pertenencia.

Las funciones de pertenencia lineales se expresan como en la ecuación (1).

μ_1 (z_1 )=∫_0^1▒(〖z_1〗^u-z_1)/(〖z_1〗^u-〖z_1〗^l )  (1)

Donde:

µ1(z1): función de pertenencia de z1

z1u y z2u: son los valores máximos de las funciones objetivo

z1l y z2l: son los límites inferiores de las funciones objetivo

Considerando las características de la tecnología en estudio11 el objetivo general del trabajo fue establecer un procedimiento general para la mejora de los indicadores técnico-económicos en la producción de yogur12 basado en las herramientas de los métodos multivariados y la optimización multiobjetivo.

Materiales y métodos

El procedimiento general se desarrolló en tres pasos:

Evaluación del proceso mediante balances de masa y energía para calcular los índices de consumo

Aplicación de métodos multivariados para obtener la relación funcional entre los índices de consumo y las variables del proceso

Empleo de la optimización multiobjetivo para establecer las mejores condiciones del proceso

Una vez identificado las operaciones, sus corrientes de entradas y salidas (frías o calientes) y el uso de agua (fría, caliente y de proceso) se plantearon los balances de masa y energía13; empleando variables del proceso de producción, especificaciones de calidad del proceso y de la materia prima. Definiéndose los parámetros que se midieron para estimar las pérdidas de materiales, los consumos energéticos y de materiales necesarios para calcular los índices de consumo del proceso.

En el segundo paso se realiza el análisis estadístico de los datos con el objetivo de caracterizar el comportamiento de las variables y luego se aplican los métodos multivariados para obtener los modelos matemáticos que relacionan los índices de pérdidas de materiales y de los consumos de portadores energéticos con las variables del proceso.

Por último, se aplica la optimización multiobjetivo para estimar la condición de operación que incremente la eficiencia.

Para aplicar los balances de masa y energía se dividió el proceso de obtención de yogur natural batido en tres etapas:

Tratamiento térmico de la leche: esta etapa se compone por la reconstitución, homogenización y pasteurización de la leche

Preparación del cultivo: incluye la reconstitución y pasteurización de la leche para el inóculo, adición del cultivo madre, refrescamiento y almacenamiento del cultivo técnico

Fermentación y envasado, se realiza la inoculación con el cultivo técnico, coagulación, enfriamiento y envasado

Como resultado de los balances de energía se obtuvieron los consumos de vapor, agua fría y agua de proceso como portador energético, que permitieron el cálculo de los índices en cada etapa de la producción de yogur. La masa de yogur obtenida en cada producción se calculó empleando la ecuación (2)

m_yogur=P_bolsas*N_bolsas              (2)

Donde:

m_yogur: Masa de producto terminado (kg)

P_bolsas: peso de envases de producto terminado (kg)

N_bolsas: número de envases de producto terminado

Se emplearon las ecuaciones (3), (4), (5) y (6) con el fin de obtener los índices de consumo de vapor y agua en el proceso.

m_(v total)=m_(v tot1)+m_(v tot2)  (3)

〖Icv〗_tot=(m_(v total)  )/m_yogur        (4)

Donde:

〖Icv〗_tot: Índice de consumo total de vapor (kg de vapor/kg de producto)

m_(v total): Masa de vapor total en el proceso (kg)

〖Icap〗_tot=m_(ap total)/m_yogur      (5)

m_(ap total)=m_(ap tot1)+m_(ap tot2)+m_(ap tot3)  (6)

Donde:

〖Icap〗_tot: Índice de consumo total de agua de proceso (kg de agua de proceso/kg de producto)

m_(ap total): Masa de agua de proceso total (kg)

Para el cálculo del índice de pérdidas de materiales se emplearon las ecuaciones (7) y (8).

Pérdidas=(m_(batido ) )-(m_yogur )         (7)

〖Ip〗_m=(Pérdidas )/m_yogur        (8)

Donde:

m_yogur: Masa de producto terminado (kg)

m_batido: Masa de leche fermentada fría (kg)

Para aplicar las técnicas de la modelación multivariada se empleó la herramienta estadística Statgraphics Centurion, según el siguiente procedimiento:

Análisis de datos y sus correlaciones

Determinación de los grupos homogéneos de datos mediante la obtención de los Conglomerados (Clúster)

Análisis de componentes principales

Ajuste de modelos por mínimos cuadrados parciales (MCP)

Mediante el análisis de los datos se obtuvieron los coeficientes de correlación entre las 14 variables medidas mediante la correlación producto-momento de Pearson, empleando un nivel de confianza de 95%.

Para la obtención de los conglomerados se utilizaron el método del vecino más cercano y la métrica de distancia euclidiana cuadrada; teniendo en cuenta experiencias anteriores de la aplicación de estos métodos, en tecnologías lácteas13. Los datos se estandarizaron para que todas las variables estuvieran dentro de un mismo intervalo de valores. El análisis se realizó para las 10 observaciones (producciones) buscando diferencias y similitudes entre ellas.

El análisis de componentes principales se emplea como paso previo al método de mínimos cuadrados parciales. Los componentes principales o factores, son combinaciones lineales de las variables medidas en el proceso estudiado y cada uno de ellos fue extraído basado en la matriz de correlaciones. Para establecer la calidad de los datos para emplear métodos multivariados se obtuvo la medida de Kaiser-Meyer-Olkin y se aplicó la prueba de hipótesis de esfericidad de Bartlett para verificar que las variables experimentales no conforman una matriz de identidad.

La selección del número de factores se realizó teniendo en cuenta que cada uno de los componentes explica una parte de la variabilidad de los datos, seleccionando el número de componentes que explica un porcentaje acumulado superior al 80 % de la varianza total de los puntos experimentales5, 6 y 13.

En el análisis por MCP se utilizó la cantidad de componentes que se obtienen del procedimiento de componentes principales, y se ajustan modelos para cuatro variables dependientes, que fueron  m_yogur, 〖Icv〗_tot, 〖Icap〗_tot, 〖Ip〗_m.

Para cada variable dependiente se obtuvieron dos modelos, uno con las variables experimentales estandarizadas centrando por la media, el cual se empleó para identificar las variables significativas estadísticamente y conocer atendiendo a la magnitud de su coeficiente, la influencia sobre las variables dependientes; mientras que su signo refleja el sentido de su efecto, si es positivo incide directamente y si el signo es negativo lo hace inversamente. Esta información se utilizó para identificar el valor experimental de cada variable independiente que favoreció más a la variable dependiente. Se obtuvo también el modelo con las variables no estandarizadas que puede emplearse para simular el proceso en estudio en sus unidades originales.

La significación estadística de los modelos se analizó con un 95 % de confiabilidad a través del valor-p de la razón de Fisher y la calidad de predicción se analizó a través del valor PRESS (sumatoria cuadrada del error de predicción). Los modelos se validaron por el método “sacar uno a la vez”, en el cual se ajusta el modelo y se deja una producción sin incluir que después se utiliza para calcular el error de predicción. Este procedimiento se repitió tantas veces como cantidad de producciones hay y, finalmente, se reporta el promedio de los errores obtenidos en dichos cálculos.

El método de optimización multiobjetivo empleado se basa en el concepto de optimización de restricciones difusas14,15 donde el grado de satisfacción (λ), es el valor que se pretende maximizar. Las cuatro funciones objetivos fueron: maximizar la masa de yogur, minimizar el índice de consumo total de vapor y de agua de proceso en la línea y minimizar el índice de pérdidas de materiales en el proceso, De acuerdo a la ecuación (1) se definieron las ecuaciones de pertenencia (9), (10), (11) y (12) respectivamente

Una vez obtenido el grado de satisfacción de cada función de pertenencia se realiza el cálculo del grado de satisfacción del proceso (λ_global) por la ecuación (13) para obtener la condición de operación que con el menor uso de vapor para pasteurizar la leche y un empleo mínimo de agua de proceso en las operaciones de enfriamiento se obtenga la mayor producción de yogur con la pérdida mínima de materiales. Esta condición será el óptimo global.

λ_global= λ_1*λ_2*λ_3*λ_4  (13)

Donde:

λ_global: grado de satisfacción del proceso

Resultados y discusión

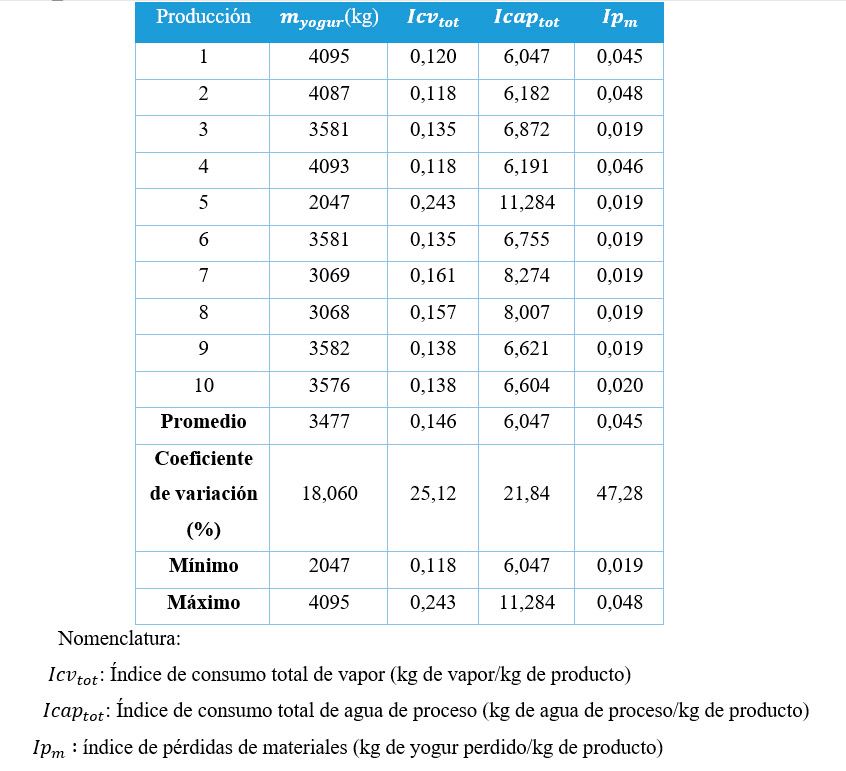
En la tabla 1 se muestra la masa de yogur que se obtuvo en las 10 producciones evaluadas obtenida por la ecuación (2) y los índices calculados, obtenidos al aplicar las ecuaciones (4), (5) y (8).

Como se puede observar en la tabla 1 los índices asociados a las pérdidas y consumos; se encuentran dispersos respecto a la media, puesto que, sus coeficientes de variación son superiores al 15 %; lo que se debe a la diferencia entre los volúmenes de leche procesada, que es de ese orden, pues el volumen mínimo fue de 2 047 kg y el mayor de 4 095 kg, con un coeficiente de variación en las 10 producciones de 18,060%. Este hecho es positivo, pues se amplía el rango de valores en que serán válidos los modelos probabilísticos que se ajusten¹³.

Tabla 1. Masa de yogur (kg) e Índices de consumo obtenidos en las 10 producciones

La determinación de los coeficientes de correlación en el análisis de datos es un paso fundamental antes de aplicar los métodos de la matemática multivariada, pues es una medida de la relación lineal entre dos variables numéricas; permitiendo identificar cuan dependientes son estas variables entre sí⁷.

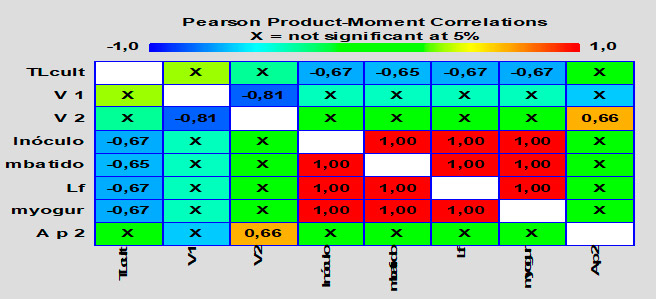
Tal y como se muestra en la tabla 2, las variables experimentales están altamente correlacionadas y estadísticamente significativas, puesto que la mayoría de los coeficientes de correlación de Pearson obtenidos, se encontraron entre 0,5 y 1 y todos con valores – p inferiores a 0,05.

 Se aprecia que hay correlaciones de variables donde existe una relación lineal positiva perfecta, lo que indica que el coeficiente de correlación es de (+1); así como también los pares donde el valor de “r” es cercano a 1, en un sentido o en otro⁶. A medida que disminuya la temperatura de la leche reconstituida a la salida del tanque de almacenamiento (); aumentará el consumo de vapor el empleado para precalentar la leche en el pasteurizador ().

De igual manera, el consumo de vapor, tienden a incrementarse juntos; al igual que la temperatura de pasteurización (), necesaria en la preparación del cultivo que tiende a aumentar con el consumo de vapor en esta etapa. Las variables relacionadas con el producto terminado tales como:  (masa a inocular de cultivo técnico en la etapa de fermentación), masa de leche fermentada (), masa de leche fermentada fría () y el número de bolsas () también tienden a incrementarse directamente como es de esperar.

Tabla 2. Correlaciones significativas (α = 0,05) entre los parámetros de operación

Nomenclatura

TLcult: temperatura de refrescamiento del cultivo (°C)

V1: vapor empleado para precalentar la leche en el pasteurizador (kg)

V2: consumo de vapor en la sección de pasteurización (kg)

Inóculo: masa a inocular de cultivo técnico en la etapa de fermentación (kg)

mbatido: masa de leche fermentada fría (kg)

Lf: masa de leche fermentada (kg)

myogur: masa de yogur ptoducido (kg)

Ap2: consumo de agua de proceso para enfriar la leche pasteurizada en la preparación de cultivo (kg)

Fuente Reporte del software

Sin embargo, entre las variables relacionadas con el producto terminado y la temperatura de refrescamiento del cultivo () existe una relación lineal pero negativa, de sentido inverso, lo que significa que un bajo valor de esta temperatura favorecerá al producto terminado puesto que habrá un crecimiento en las variables asociadas con el mismo.

El hecho de haber obtenido correlaciones estadísticamente significativas entre las variables medidas justifica el procesamiento mediante los métodos matemáticos multivariados. El análisis de conglomerados permite identificar el grado de homogeneidad entre los datos experimentales, por lo que cuando se aplica a las observaciones por producción revela la similitud o diferencia entre las condiciones de operación durante el período de análisis^7,13. En la figura 1 se muestra el dendograma obtenido para las producciones en estudio.

El dendograma muestra que entre las corridas 9 y 10 se obtiene la menor distancia de agrupación, siendo significativo que ambas tienen un volumen de producción igual a 3500 L; estas como grupo, se asemejan a las observaciones 3, 7, y 8 que presenta la siguiente distancia de agrupación; pero resultaron ser similares, puesto que fueron producciones que trabajaron bajo semejantes condiciones de operación. Las producciones 1 y 2 como tienen un volumen de producción igual a 4000 L resultaron semejantes entre sí; las cuales presentaron una distancia de agrupación pequeña con la corrida 6, debido a que en esos días se llevó a cabo el proceso, con iguales condiciones de operación y con la observación 4, puesto que esta última tiene el mismo volumen de producción, estando así conformado el primer conglomerado por esas 9 observaciones. El segundo grupo resultó estar conformado por la producción 5 que presenta como diferencia fundamental que se trabajó con un volumen de producción igual a 2000 L.

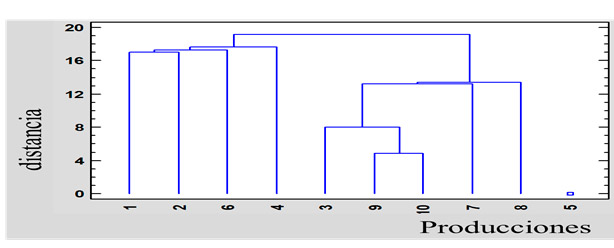
Figura 1. Dendograma de las variables asociadas a las producciones evaluadas

Fuente Reporte del software

Por los resultados que se obtienen, es evidente que el volumen de producción es un factor que tuvo mucho peso en la clasificación por grupos, lo que es de esperar, pues el resto de las variables asociadas a los consumos tomaran valores en dependencia a la masa total a procesar. Las condiciones bajo las cuales se operaron esas producciones, es otro factor a resaltar entre los grupos homogéneos; siendo la temperatura de la leche pasteurizada fría una condición de operación común en la clasificación por grupos, lo que es muy importante ya que esta variable tiene una marcada influencia en la calidad del producto terminado.

Es importante destacar la utilidad de este método multivariado para identificar semejanzas y diferencias en una misma línea productiva.

El análisis de Componentes Principales se emplea como paso previo al método de mínimos cuadrados parciales para tener información respecto a los modelos matemáticos a ajustar^6,13. El propósito de este análisis es obtener el menor número de combinaciones lineales de las variables que expliquen el mayor por ciento de variabilidad en los datos.

Con las variables no lineales de la base de datos (TLcult, V1, V2, Inóculo, Mbatido, Lf, myogur, Ap1 y AP4) se obtuvo una medida de Kaiser-Meyer-Olkin igual a 0,62, que por ser superior a 0,5 indica que pueden emplearse el análisis factorial, dado que las correlaciones entre los pares de variables pueden ser explicadas por otras variables. En la prueba de hipótesis de esfericidad de Bartlett se obtuvo un valor de chí-cuadrado igual a 800, con un valor- p inferior a 0,05, lo que indica que la matriz de correlaciones no es una matriz de identidad, corroborándose que pueden emplearse los datos experimentales con métodos multivariados.

En la tabla 3 se muestra el porcentaje de la varianza explicada por cada componente y el acumulado, siendo de notar que 4 componentes explican el 95,102% de la variabilidad en los datos originales, lo cual puede considerarse suficiente⁵. Además, con un quinto componente, se explica un 3% adicional de la variabilidad de los datos, pero sería un modelo más complejo.

Con vistas a obtener la relación funcional entre las variables independientes y las 4 dependientes teniendo en cuenta los resultados obtenidos en el análisis de componentes principales, se aplicó el método de mínimos cuadrados parciales con cuatro componentes⁶. En las tablas 5 y 6 se muestra el análisis de varianza y de calidad de ajuste del modelo para . No se muestran los resultados en el análisis de varianza y de calidad de ajuste del modelo para las variables , ,, pues fueron similares.

Tabla 3. Porcentaje de la varianza explicada por cada componente y la varianza acumulada

Componente número	Porcentaje de la varianza explicada	Porcentaje acumulado
1	56,103	56,103
2	20,832	76,935
3	13,815	90,750
4	4,352	95,102
5	3,207	98,309
6	1,686	99,995
7	0,004	100,000
8	0,000	100,000
9	0,000	100,000

 

Los resultados obtenidos demuestran que el modelo ajustado por MCP para la variable  presentó buena calidad de ajuste para un 95 % de confiabilidad, con valores-p inferiores a 0,05 que es el límite superior para la prueba de Análisis de varianza. Es de notar que se trabajó con 9 grados de libertad, siendo14 variables independientes y 10 producciones, lo que resulta una de las ventajas de este tipo de ajuste, pues los grados de libertad se refieren al número total de componentes a incluir en el modelo.

           Tabla 5. Análisis de varianza para

Fuente	Suma de cuadrados	Gl	Cuadrado medio	Razón-F	Valor-p
Modelo	3,5467	4	0,8866	565,916	0,000
Residuos	0,0078	5	0,0015
Total (corr.)	3,5545	9

Fuente Reporte del software

         Tabla 6. Calidad de predicción del ajuste de mínimos cuadrados parciales

Componente	% de variación en Y	R-cuadrada	Cuadrado medio (PRESS)
1	93,63	93,63	5,22 x 10-2
2	4,97	98,61	2,66 x 10-2
3	1,00	99,61	1,83 x 10-2
4	0,16	99,77	1,66 x 10-2

Fuente Reporte del software

Con cuatro componentes se obtuvo un error de predicción pequeño (PRESS), lo que manifiesta muy buena calidad en la predicción, siendo el valor de R-cuadrada igual a 99,77%, lo que indica que puede considerarse totalmente explicado el error experimental en los datos.

El modelo obtenido con los coeficientes no estandarizados para cada variable dependiente, se muestran a continuación:

Donde:

TLr: temperatura de la leche pasteurizada en la etapa de recibo (°C)

TLp: temperatura de la leche pasteurizada en la etapa de intercambio térmico  (°C)

TLpf: temperatura de la leche pasteurizada fría en la etapa de intercambio térmico (°C)

TLp1: temperatura de la leche pasteurizada en la etapa de preparación de cultivo técnico (°C)

TLpf1:temperatura de la leche pasteurizada en la etapa de fermentación de cultivo técnico (°C)

TLcult: temperatura de refrescamiento del cultivo (°C)

TsLf: temperatura de la leche fermentada fría (°C)

V1: vapor empleado para precalentar la leche en el pasteurizador (kg)

V2: consumo de vapor en la sección de pasteurización (kg)

V3: consumo de vapor en la etapa de preparación de cultivo técnico (kg)

Ap1: consumo de agua de proceso en la etapa de intercambio térmico (kg)

Ap2: consumo de agua de proceso para enfriar la leche pasteurizada en la preparación de cultivo (kg)

Ap3: consumo de agua de proceso para refrescar el cultivo técnico (kg)

Ap4: consumo de agua de proceso en la etapa de fermentación (kg)

Inóculo: masa a inocular de cultivo técnico en la etapa de fermentación (kg)

Lf: masa de leche fermentada (kg)

mbatido: masa de leche fermentada fría (kg)

myogur: masa de yogur ptoducido (kg)

Peso: peso del envase del producto terminado (kg)

Nbolsas: número de envases de producto terminado (-)

En la Tabla 7 se muestran los resultados de los valores predichos de las 10 producciones y sus correspondientes residuos (errores de estimación), obtenidos en el modelo para la variable dependiente .

Se aprecia en la tabla 7 que los residuos son muy pequeños, en el caso de  , el mayor valor es 0,046 y el menor 0,005 (en valores absolutos), lo que manifiesta la calidad en la predicción con este modelo.

En el caso de las variables 𝐼𝑐𝑣𝑡𝑜𝑡 , 𝐼𝑐𝑎𝑝𝑡𝑜𝑡 , 𝐼𝑝𝑚 los residuos en los tres modelos resultaron también pequeños, siendo los mayores errores de predicción iguales a -0,0060, -0,329 y -0,0083 respectivamente. Lo importante de tener esas predicciones con errores tan pequeños; es que se obtendrán buenos pronósticos cuando se empleen para evaluar otras combinaciones en las condiciones de producción.

Mediante el análisis de los coeficientes estandarizados fue posible identificar el peso con que inciden, ya sea en sentido directo o inverso; cada una de las variables independientes sobre las dependientes, tal como se presenta en la tabla 8.

                  Tabla 7. Valores obtenidos en el modelo para

Producción	𝑚𝑦𝑜𝑔𝑢r	Predicho	Residuo
1	4095	4104	-9 x 10-3
2	4087	4092	-5 x 10-3
3	3581	3606	-2,5 x 10-2
4	4093	4075	1,7 x 10-2
5	2047	2069	-2,2 x 10-2
6	3581	3627	-4,6 x 10-2
7	3069	3055	1,3 x 10-2
8	3068	3027	4 x 10-2
9	3582	3535	4,6 x 10-2
10	3576	3584	-8 x 10-3

Las variables , ,  y  presentan un peso significativo sobre las cuatro variables dependientes. Las tres primeras variables están estrechamente relacionadas con el producto terminado, incidiendo directamente sobre la masa de yogur y de forma inversa sobre los índices de consumo de vapor y agua, esto es un comportamiento esperado, pues cuando el proceso opere con menos vapor para pasteurizar la leche, se requerirá menos agua de proceso en las operaciones de enfriamiento, para obtener la misma producción de yogur.

A excepción de estas variables, la temperatura de refrescamiento del cultivo incide directamente sobre esas variables dependientes; un bajo valor de esta temperatura favorecerá al producto terminado por lo que, habrá un crecimiento en las variables asociadas con el mismo; este comportamiento reafirma lo explicado anteriormente; por tanto, la temperatura de refrescamiento incidirá inversamente sobre la masa de yogur.

Sin embargo, estas cuatro variables independientes inciden de forma directa sobre el índice de pérdida de materiales, lo que es de esperar; ya que tanto el cultivo iniciador como la temperatura de incubación, las condiciones de procesamiento y las propiedades de composición de la base de la leche; son parámetros que pueden provocar la pérdida de material de este producto lácteo, debido a que, afectan el sabor y la textura del yogur, dichos factores son los más pronunciados que influyen en la calidad y aceptación del producto terminado.

Por ende, se debe tener un control riguroso sobre ellas, puesto que las mismas, pueden modificar significativamente a dichas variables dependientes y provocar cambios en las condiciones de operación, que podrían afectan el sabor y la textura del yogur y conllevar a la disminución del volumen de producción; generando tanto pérdidas materiales como económicas, ya que, un alto consumo de vapor y agua de proceso en la línea podría llegar a incurrir en gastos por servicios auxiliares y encarecer el proceso de producción de yogur natural batido.

A partir de toda la información obtenida del proceso en estudio, basado en los métodos de la matemática multivariada y en particular de los modelos de MCP, es evidente que existen condiciones de operación con las que se obtienen mejores resultados tanto en el aspecto técnico como económico, referido a la reducción del consumo de vapor, pero es conveniente realizar un análisis basado en la integración de procesos, que incluya varios indicadores de eficiencia. Una vía para seleccionar estas condiciones es la optimización multiobjetivo^14,15,16.

En la tabla 9  se muestra el grado de satisfacción de cada función de pertenencia y la   del proceso, obtenidos a partir de la ec.5 a la ec.8. Otros autores han aplicado otros tipos de modelos más complejos con resultados igualmente satisfactorios^{17, 18, 19, 20}.